or How Large Numbers Generate Order
Originally published on ordersogmagnitude.org
The music is loud, the lights are out, and you’re on your third glass since entering the club. Your friends? They’re somewhere, probably twice as glazed as you. You dance and jump and move around without any real sense of direction. Your legs cross, changing the path where you were going whenever a stranger bumps into you. You can’t make out the music, but the compassed beat of the base, synchronized with the movements of everyone around you, creates a collective euphoria to the point where there’s no more you. You are the crowd, and the crowd is you.
Why are humans made of so many atoms?
I recently came across this question by reading a small book written by a very popular physicist called Erwin Schrödinger who’s well known because of a thought experiment involving a cat in a box. In this little book titled “What is Life,” he apologetically dives into the much different field of biology. Apologetically because, as a physicist, he was likely to make mistakes on his accounts of biology, the same way that I – as a biochemist who recently got into biophysics – am bound to make mistakes when it comes to physics. That being said, let me apologize in advance to my physicist friends if my takes on the physical concepts presented here are incomplete.
I firmly believe that understanding small seemingly useless concepts, such as the one I’m summarizing here, can unconsciously contribute to groundbreaking realizations. After all, ideas are made to create new ideas. For this reason, I want to translate Schrödinger’s attempt (and perhaps success) at answering the question in the title. Despite being a fantastic science communicator, Schrödinger’s language in the original text is quite philosophical and requires much concentration. So, here’s my summary of his fascinating answer to the question, “Why are living organisms so large compared to the size of an atom?”
A football field-sized cell.
It’s helpful to start this conversation by saying just how tiny an atom is. The average human cell is about 0.1 mm in diameter. That’s ten times smaller than the smallest measure in an ordinary ruler. Imagine that you can scale that cell up to the size of a human1. For a cell of that size, an atom would still be smaller than your average human cell.
Still can’t visualize it? All right. Let’s scale that up even more. Imagine you scale your average human cell to have a diameter equal to the length of a soccer field, which is 125 meters (or 136 yards). If, somehow, with some crazy magic, we get a cell as big as a soccer field, the atoms composing that cell would only be as big as a grain of sand2.
In his original text, Schrödinger illustrates the massive number of atoms in everyday objects by quoting an example given by Lord Kelvin3. It goes as follows. Imagine that you can tag all the atoms in a glass of water. Then, pour the tagged atoms into the ocean and mix all the water of the seven seas so that they are distributed equally across the globe. If you then filled a glass with water out of any ocean on the planet, you would find roughly one hundred of your tagged atoms within your new glass!
Of course, if you repeated this experiment several times, you wouldn’t get exactly 100 atoms with every attempt. Sometimes you might get 95, 88, 102, or 112 atoms. But very rarely would you find as few as 50 or as many as 150 atoms. The inaccuracy expected with each measurement is defined by some pretty general laws of statistics that we have to cover to answer our original question fully.
A tiny bit of statistics
Or the √n rule.
Statistically speaking, the deviation in the results of a physical law is expected to be in the order of √n, where n is the number of samples in our experiment. Therefore, we expect to see a deviation of plus or minus 10 atoms per glass of water in the glass of water experiment, which means that most of our experiments would have between 90 and 110 tagged atoms in the final filled glass. So, you have a 10% inaccuracy with every measurement.
Now, imagine that you’re filling 100 glasses of water. In this case, you expect to collect around 10000 tagged atoms plus or minus 100 atoms, a 1% inaccuracy. In the same way, if you filled up a container large enough to collect one million tagged atoms, you’d expect an inaccuracy of plus or minus 1000 atoms, or 0.1%.
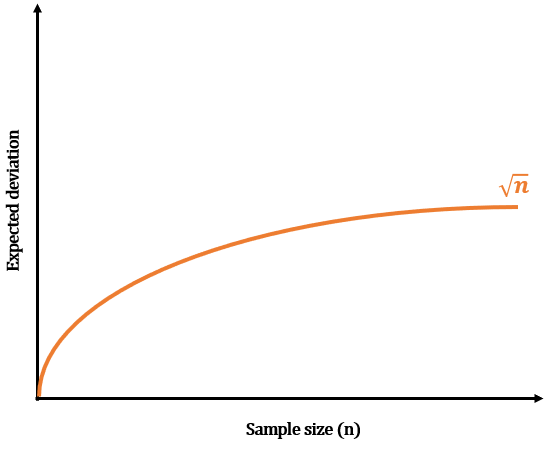
You can probably see a pattern here. The larger the number of atoms we expect to count, the more accurate our measurements will be! Hence, for any system to operate with fairly accurate laws, it must contain a fairly large number of atoms. And that’s where the answer to our initial question starts to take shape.
You’re being bombarded — all the time.
If you stop to think for a second, since everything is made of atoms, you’re a clump of atoms flowing in a big soup of atoms. Many carbon dioxide (CO2), nitrogen, and oxygen molecules are constantly entering and exiting your lungs. Yet, it doesn’t feel like thousands of molecules made of 2-3 atoms each are hitting the walls of your airways.
What would life be like if we could sense every atom interacting with our bodies? It would be hell on earth! Such a person would never be able to form any complex thoughts (if any thoughts at all) as they would be overwhelmed by the constant noise that hits their skin without a break.
Thankfully, we do not sense every atom that surrounds us. That’s because our bodies interact with the world around us in an extremely complex way. The main point here is that such levels of complexity in an intrinsically disordered universe can only arise with an excessive number of disordered elements. As we saw in the previous section, the precision of physical laws depends heavily on the number of atoms intervening. All atoms behave in a highly disordered way. Atoms move around vigorously, following random patterns with speeds varying depending on the temperature4. However, many things in nature follow some very precise rules despite everything being made of particles that move at random (the human body being an extreme example of this). Let’s look at a simple model that most of us are familiar with to try and illustrate how many particles can give rise to new, more organized properties.
Drunk molecules in a rave
Or why food colourant spreads in a glass of water.
Atoms move very much like a blindfolded person walking in a room without any sense of direction. Try this at home: take a glass of water and add one or two droplets of red food colouring5. Do not steer the glass. If you leave it on the table long enough, all the water will eventually become red. What happened? We’ll usually say that dye diffused through the water, going from a region with a lot of dye to an area with little dye until everything is equal.
But how? Do the colourant molecules have some sort of intelligence helping them find directions towards smaller dye concentrations? Is there a “concentration field” pulling the molecules toward locations with less dye? No. It’s all about numbers. If you stare at the water, it looks like the food colourant constantly moves toward colourless spaces. But that’s an illusion caused by the enormous number of molecules that make the dye front. If, instead, you could look at a single molecule, you would be surprised to see that it’s not moving in any specific direction. It’s moving randomly, leftwards, upwards, downwards, then upwards again. It doesn’t care where it goes. It just goes.
Every dye molecule moves quite independently from each other, and they rarely meet. Instead, each one is constantly being pushed around by the water molecules, gradually moving in unpredictable directions. Sometimes they go towards where there is more colour, and sometimes towards where there is less.
Take a look at the drawing below. Here, we’re assuming that we can separate the glass of water into tiny slices with close to constant concentrations of food colouring. If you consider a single slice, you’d expect to see as many molecules exiting the cut toward the right as you expect toward the left, since the molecules move randomly.
Now, consider two slices separated by a plane, where the slice on the left has twice as many molecules as the slice on the right. You would see molecules crossing the plane in both directions. There are molecules going toward the right, and there are molecules going toward the left. But, because the slice on the right has twice as many molecules than the slice on the left, there will be twice as many molecules crossing toward the right than toward the left.
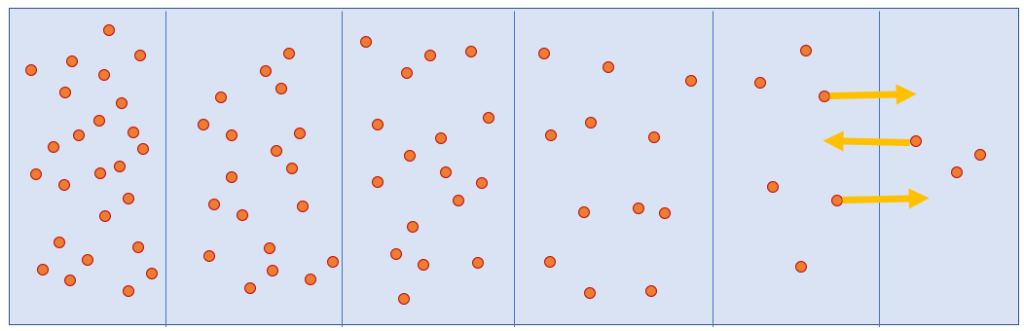
Of course, these molecules are not atoms, but they’re small and light enough to be influenced by the impacts of the water molecules. Like these molecules, atoms constantly vibrate and move because of the universe’s heat. Yet, despite continually moving and interacting at random, at high enough numbers, a new, more organized property emerges from these atoms, much like how the diffusion of molecules appears to be organized.
It just takes that many atoms to reach the level of complexity of a human body
Or “Too long; I didn’t read.”
If someone asked me why humans are made of so many atoms, I’d answer that it is “because you just need that many atoms to reach the level of complexity that a human body has.” But now I see how that is a terrible answer. That answer barely rephrases the initial question. If someone asked me, “Why do monkeys like bananas,” they would be pretty disappointed if I said that it is because they think bananas taste good. Schrödinger, of course, did a way better job answering the question.
It does not take a brilliant mind to observe that our bodies are incredibly complex machines. However, despite being marvellous machines that can accomplish wonders, they are only made of mindless disordered atoms. Each atom is “drunk” with the heat of the universe. They move around without any real sense of direction. Their “legs” cross occasionally, changing the direction where they go whenever another atom bumps into them. They can’t make out the “music,” but the compassed beat of the base, synchronized with the movements of every other atom, creates a collective euphoria to the point where there’s no more atom. The atoms are you, and you are the atoms.
1 For this exercise, I am assuming that our scaled-up cell has a diameter of 1.70m, which is the height of an average male in North America.
2 With some quick Google search, you’ll find that atoms have an average radius of 0.1nm, while cells have an average radius of 100µm. In other words, an atom is 106 times smaller than a cell. Your average grain of sand has a radius between 0.0625 and 2mm. So, it’s not crazy to think of a grain of sand with a 0.125mm radius. Since a soccer field is 125 meters in length, a grain of sand with a size of 0.125mm would be 106 times smaller than that soccer field.
3 Yes, yes. That OG scientist to whom the temperature unit is named after.
4 Temperature, after all, is nothing more than a measure of how fast atoms are moving.
5 Yes, it has to be red. Everyone knows that red water is way more tasty than blue, green, or – ugh – yellow water.


